Recapitulation of Ant Colony and Firefly Optimization Techniques

Anuradha^*, Kshitiz Adlakha

CSE&IT Dept., ITM University, Gurgaon, India

Abstract

This paper presents an analysis done on ACO and FFA optimization algorithms. Optimization algorithms have been used successfully to solve various problems in different areas. These algorithms are considered an important part of Swarm Intelligence, which refers to the social interaction of swarms of ants, termites, bees, termites and flock of birds. The methods used for the comparison are Max-Min Ant System, Ant Colony System, Rank-based Ant System and various hybrids/modified firefly algorithms. ACO and FFA can be modified and hybridized to solve diverse engineering problems. In most cases, the results provided by these algorithms meet the expected output.

Keywords

Ant, Firefly, ACO, Swarm Intelligence, Meta-Heuristic, Pheromone

Received: July 1, 2015
Accepted: August 8, 2015
Published online: August 26, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

Problems of optimization are found in almost all industries as well as in the scientific community. Logistical traffic routing, reducing the cost of manufacturing of products, travelling salesman problem are all examples of optimization problems. In the creation of Integrated Circuits (ICs) using the VLSI method, the placing of components of the board such as to maximize energy efficiency, minimize production cost is an important problem.

Over the past 10 years, Swarm Intelligence [1] has become very popular. It includes the employment of multi-agent systems that are based on the actions of real world insect swarms for solving problems. The swarms that are observed show coordinated behaviour to proceed towards their goals, like searching for food and building sophisticated nests. This coordinated behaviour is a result of the interactions between the individuals of the swarms. Different insects interact in different ways with each other. Ants interact with a chemical pheromone trails to find the shortest path to their food sources, whereas bees interact with each other with a so-called ‘waggle dance’ where the a few bees known as ‘bee scouts’ lead the colony of bees towards the new food sources discovered by them. The bee colony must be aware of when to exploit the existing food sources and when to find the new ones, so as to maximize the nectar intake and minimize the scavenging effects. Many of the decisions like reproduction, division of important tasks are made in a distributed manner based on the native information obtained from the exchanges with their transitional surroundings [2].

2. Ant Algorithms

Ant algorithms and firefly algorithms are two of the most recent techniques developed in the field of swarm intelligence. Ant algorithm was originally developed in 1996 by Dorigo, Maniezzo, & Colorni, [3] while Firefly algorithm was developed by Yang in 2008 [4]. Both of these algorithms were later formalized into meta-heuristics. These algorithms are inspired by nature and can be applied to solve the hardest of optimization problems, including NP-hard problems. Fig 1 shows the shortest path followed by ant from source to food destination.

Fig. 1. Shortest Path Experiment.

The searching behaviour of ants in the wild was the original motivation towards the development of ant algorithms. Ants interact with each other by laying a pheromone trail, which they tend to follow. Experiments in the past have shown that ants are more likely to follow a trail with a greater concentration of pheromone.

The above given figure shows an experiment, called the "shortest path" experiment [5], conducted to show the path followed by ants when they leave their nests in search for food. In the figure, ‘N’ represents the nest of the ants and ‘F’ represents the food. There are two possible paths to reach to the food from the nest, NDCBF and NDHBF. Initially, when the ants leave in search for food, half of the ants follow the left path and half of them follow the right one. The ants following the left path reach the food source quicker. As soon as an ant collects the food from the source it tracks its way back to the nest through the pheromone trail laid down earlier, on its way to the food source, while laying pheromone again, and thus strengthening the pheromone trail along the left path. Now any ants leaving the nest or returning from the food source are more likely to follow the path on the left, due to the high concentration of pheromone on this path.

3. Applications in Computer Science

This behaviour of ants can be achieved in the computational world with the use of artificial ants (agents) that communicate through artificial pheromone trails.

An artificial ant should have the following properties [6]. It should have an interior memory that stores all the previously visited locations. Each ant should try to find a likely solution to the problem starting from the initial state, iterating through its search environment. A specific pheromone update rule should govern the amount of artificial pheromone each agent/ant deposits while moving.  Pheromone may be deposited with states or otherwise, during state transition. While the solution is being created, pheromone may deposit at each state transition. This is called the ‘online step by step pheromone trial update’. On the other hand, when ants retrace their path when a solution has been created and only then deposit pheromone on their trails, it is called ‘online delayed pheromone update’.

Along with these properties on the ants of the wild, artificial ants have extra features which help them in advancing their performance. Some of these features that have been widely used in the past are local search and candidate list. The first ant algorithm was developed by Dorigo et al. in 1996 [3]. It was called the ‘Ant System’. It was successfully applied to the classic Travelling Salesman Problem (TSP). A TSP problem involves finding the shortest length to travel each town of a set of towns, M. The success of this algorithm led to the development of a lot of other ant algorithms. The first of these was the ACO meta-heuristic. It was developed in the 1999 by Dorigo & Di Caro [8]. It described the overall way of finding a solution to combinatorial problems by estimated solutions based on the standard behaviour of ants. Given below in Fig.2 is the algorithm of ant colony meta-heuristic:

Fig. 2. The ant colony meta-heuristic.

The main ACO algorithms are the Max-Min Ant System, Ant Colony System and Rank-based Ant System. In the Max-Min Ant System (MMAS) algorithm [7], the pheromone trail is updated by only the best ant-updates and unlike the original Ant System, the pheromone update function is bound.

In the Ant Colony System [9], the pheromone update function is different from the one in the original Ant System. Just like the ants in the wild, in ACS a local pheromone update is applied along with the update of pheromone at the end of the each offline pheromone update. This offline pheromone update is applied by the iteration-best or best so far ant only, which is similar to the MMAS algorithm.

In the Rank-based Ant System [10], the solutions of each ant are ranked in a decreasing order of the quality of their tour length. The pheromone deposited by each ant depends upon the rank of the ant. The global-best solution receives extra amount of pheromone depending on the quality of the solution.

Computational results (taken from Stutzle et al. (2000) [7]) displaying the optimum results of four ant algorithms as applied to three different TSP instances is shown in Fig.3.

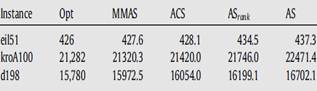
Fig. 3. Computational Results of famous ant colony optimization algorithms.

4. Advanced Ant Algorithms

Over the past few years, there has been a lot a development in the field of Optimization, eventually leading to more specialized ant algorithms. Following the research there has been a significant rise in the applications of ant optimization techniques. Below are some notable applications of ant optimization.

The Protein Folding Problem: One of the most complex NP hard combinatorial problem yet fundamental in computational molecular biology is protein folding problem. Predicting the native structure of proteins contained in amino acidic sequence by understanding and analysing the bio-cellular level structure in huge conformational space in is highly expensive approach. The Sequence of Hydrophobic and Polar residues from the amino-acidic sequences in proteins are represented as H and P respectively. The solution to Protein folding problem for both 2D [11] and 3D [12] lattices is Ant Algorithms. Using the Gibbs hypothesis the native state of protein is the one with lowest Gibb’s free energy - the number of topological contacts between hydrophobic amino-acids that are not neighbours gives the conformation Gibb’s free energy.

Conformation c, h such H–H contacts, it has free energy

E(c) = h. (-1).

Digital Image Processing using boundary detection algorithms use the pheromones pheromone used in ant algorithm [13], [14]. Boundary detection algorithm along with clustering algorithms [15], [16] is used for the low level image segmentation processes using ant algorithmic techniques. The digital image is the ant arena or the search space for ants, moving around the arena using the pixels in distinct pixel-wise mode. To achieve boundary detection, locating and mapping out the boundary within the image using the heuristic information weighs higher the probability of an ant moving from its current location to the allowed surrounding pixel that has the greatest boundary characteristics, here comes the pheromone characteristic from Ant Algorithm considering every movement to a new pixel in an image depositing pheromones, change in the image gradient and pheromone evaporation occur at a fixed rate per iteration. The pheromone trail leads to the boundary detection considering the transition rule as heuristic function, as the ants converging at the boundary starting at the random positons with the increasing ants following the pheromone trail maps the leaf boundary. Considering the assertions in this application of Ant Algorithm comparing to typical original ant algorithm; final solution is achieved using the pheromones as well as guiding the ant movement and single ant or one ant cannot achieve this boundary detection for image. Clustering mechanism uses ant algorithm as a standard tool for mapping pixels to cluster in the search space; ants searches for low grayscale regions and in an area away from segmentation.

Analysis of large amounts of data using various data mining and warehousing techniques by performing various operations such as data clustering, data classification and data forecasting with the aim to find valid patterns and relationships among large data sets leading to extract right knowledge from data [17], [18]. Later development in the field of data analysis, Ant algorithms are also being used as a purpose to deal with classification of large amount of data. Based on the sets of predefined classed each case (object, record or instance) is assigned to a class based on the value of the attributes for the case.

5. Firefly Algorithms

There are more than 2000 species of fireflies in the world, which live around in warm environments and are most active during the summer. They have been a topic of research for a long time now and a lot of research papers have been written about them.

Their most distinguishing feature is their flashing light which is produced a biochemical procedure bioluminescence. They use this light to attract other partners for mating and for warning off potential predators. Usually, the flying males make the first signal trying to attract the flightless female fireflies on the ground. Females, in turn, emit continuous or flashing lights, which are generally brighter than the lights produced by male fireflies. This flashing light has served the basic foundation towards the development of the firefly algorithm.

The FA was given by Yang in 2008 [4], which described the classical firefly algorithm. It was a very efficient optimization algorithm which was able to derive more optimal solutions in the given search space simultaneously.

The algorithm formulated by Yang is given below by Fig 4:

Fig. 4. Pseudo Code of Firefly Algorithm.

Clauses used:

All fireflies are unisex.

Attraction of a firefly is proportional to their light intensity.

The intensity of the light of a firefly is determined by the fitness function.

6. Classification of Firefly Algorithms

There are a lot of variants of the popular firefly algorithm; therefore a classification system is essential. The most common way of classifying firefly algorithms is one the basis of the settings of their strategy parameters [19]. Choosing these parameters is a crucial task for the developers, as they directly affect the efficiency of the algorithm. Along with these parameters, other things like what features or modules are modified also determine the behaviour of the FA.

The classification can be done on the basis of

1.   Features or modules that are modified:

•     Depiction of fireflies (binary, real-valued)

•     Population structure (swarm, multi-swarm)

•     Calculation of the fitness function

•     Determination of the best solution (non-elitism, elitism)

•     Movement of fireflies (uniform, Gaussian, Lévy flights, chaos distribution)

2.   Way of modification:

•     Deterministic

•     Adaptive

•     Self-adaptive

3.   Range of modifications:

•     A component of the firefly

•     The whole firefly

•     The complete population

Another way of classifying the classic firefly algorithms is to divide them into two parts, modified and hybrid. Hybridization was first done when problems arose in finding the appropriate solution of some optimization problems. Fig. 5 shows the categorization of famous firefly algorithms:

Fig. 5. Classification of Firefly Algorithms.

7. Efficiency of Firefly Algorithms

The firefly algorithms are one of the most efficient algorithms at solving classification and optimization problems. The reasons for that are many. We can point the major explanations for its success by analysing its features.

The first feature of FA is that it can automatically split its population into subdivisions on the basis of the fact that attraction by nearer neighbours is higher than the ones that are far. This helps in FA in solving multi-modal optimization problems more efficiently.

The second feature of FA is that it does not use historical individual best or an explicit global best which prevents premature convergence like those in particle swarm optimization (PSO) [26].

Firefly algorithms have the ability to control their scaling parameter which helps them adjust to the problem landscape and switch their modality. Velocities are not used in firefly algorithms, thus there are no problems associated with that unlike the particle swarm optimization.

After analysing all these features, we can consider FA to be a generalization of PSO, simulated annealing and differential evolution. FA takes benefits from all of these 3, hence performing in an extremely efficient manner.

8. Applications of Firefly Algorithms

Firefly algorithms are used in various fields for answering optimization and classification problems along with several engineering problems.

In the field of optimization, FA is used in combinatorial, constrained, multi-objective, continuous, dynamic and noisy optimization. Most of the past publications about the firefly algorithm, like [20,21,22,23,24] relate to continuous optimization problems.

In the field of classification, FA is used in data mining, neural networks and machine learning. Even though classifications can be measured as optimization, Holland [25] penned that learning, as component part of classification, is looked at as a procedure of adaptation to a particularly unknown environment, not as an optimization problem.

FA is used in almost all branches of engineering. It has become of one of the most important technologies in engineering today. The scope of the reviews done on firefly algorithms in engineering practices is very large. Industrial optimization has the greatest number of papers written about in engineering applications. It is followed by image processing and then antenna design [27] [28]. Fig. 6 shows the various areas covered by Firefly algorithms:

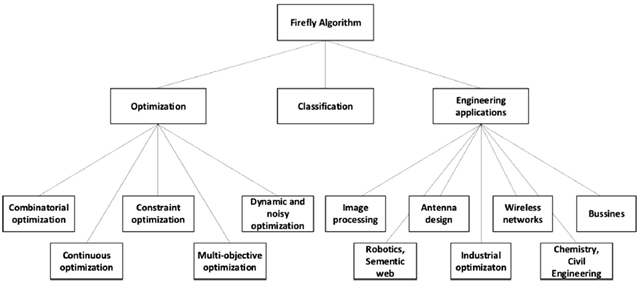
Fig. 6. Various areas covered by Firefly algorithms.

9. Conclusion

Both FA and ACO algorithms have come a long way from their inception. Today, they are practically used in every domain of science and industry. This paper has briefly detailed some of the developments and applications of both of these algorithms with the aim to make them easy to understand for everyone.

Due to their large scope of applications, these algorithms are bound to move forward and make even more progress in the coming future. Hybridizing them with other techniques will lead to development of even more efficient algorithms that can be used to solve dynamic problems.

This paper shows that ACO and FA are easy to understand, flexible and can be used in a lot of domains. At the same time, it also promotes future development of these algorithms to solve the unanswered questions and deal with even more harder challenges.

References

1. C. Blum, X Li, Swarm intelligence in optimization, Swarm Intelligence: Introduction and Applications, Springer Verlag, Berlin, 2008, pp.43–86.
2. M. Beekman, G.Sword, S.Simpson, Biological foundations of swarm intelligence, Swarm Intelligence: Introduction and Applications, Springer Verlag, Berlin,2008, pp.3–41.
3. Dorigo, M., Maniezzo, V., & Colorni, A. (1996). Ant System: Optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics – Part B, 26, 29–41.
4. X.S. Yang, Firefly algorithm, Nature-Inspired Metaheuristic Algorithms 20 (2008)79–90.
5. Goss, S., Aron, S., Deneubourg, J. L., & Pasteels, J. M. (1989). Self-organized shortcuts in the argentine ant. Naturwissenschaften, 76, 579–581.
6. Cordon, O., Herrera, F., & Stutzle, T. (2002). A review on the ant colony optimization metaheuristic: Basis, models and new trends. Mathware and Soft Computing, 9(2–3): 141 175.
7. Stutzle, T., & Hoos, H. H. (2000). Max–min ant system. Future Generation Computer Systems, 16(8), 889–914.
8. Dorigo, M., & Di Caro, G. (1999). The Ant Colony optimization metaheuristic. New Ideas in Optimization (pp. 11–32).
9. Dorigo, M., & Gambardella, L. M. (1997). Ant Colony System: A cooperating learning approach to the travelling salesman problem. IEEE Transactions on Evolutionary Computation, 1(1), 53–66.
10. Bullnheimer, B., Hartl, R. F., & Strauss, C. (1996). A new rank-based version of the Ant System: A computational study. Central European Journal for Operations Research and Economics, 7(1), 25–38.
11. Shmygelska, A., Hoos, H. H. (2003). An improved ant colony optimisation algorithm for the 2D HP protein folding problem. In Advances in artificial intelligence: 16th Conference of the Canadian society for computational studies of intelligence, Halifax, Canada, AI 2003 (page 993).
12. Findova, S. (2006). 3D protein folding problem using ant algorithm. In Proceedings of BioPS international conference, Sofia, Bulgaria (pp. 19–26).
13. Fernandes, C., Ramos, V., & Rosa, A. C. (2005). Self-regulated artificial ant colonies on digital image habitats. International Journal of Lateral Computing, 2(1), 1–8.
14. Ramos, V. & Almeida, F. (2000). Artificial ant colonies in digital image habitats – a mass behaviour effect study on pattern recognition. In Proceedings of ANTS’2000
15. Channa, A. H., Rajpoot, N. M., & Rajpoot, K. M. (2006). Texture segmentation using ant tree clustering. In 2006 IEEE international conference on engineering of intelligent systems (pp. 1–6).
16. Ouadfel, S., & Batouche, M. (2002). Unsupervised image segmentation using a colony of cooperating ants. In BMCV ’02: Proceedings of the second international workshop on biologically motivated computer vision (pp. 109–116). Springer-Verlag.
17. Fayyad, U. M., Piatetsky-Shapiro, G., & Smyth, P. (1996). From data mining to knowledge discovery: An overview. In Advances in knowledge discovery and data mining (pp. 1–34). Cambridge, MA: AAAI/MIT.
18. Edelstein, H. A. (1999). Introduction to data mining and knowledge discovery (3rd ed.). Two Crows Corporation.
19. A. Eiben, J. Smith, Introduction to Evolutionary Computing, Springer-Verlag, Berlin, 2003.
20. X.S. Yang, Firefly algorithm, stochastic test functions and design optimisa- tion, International Journal of Bio-Inspired Computation 2 (2) (2010) 78–84.
21. X.S. Yang, Review of meta-heuristics and generalised evolutionary walk algorithm, International Journal of Bio-Inspired Computation 3 (2) (2011) 77–84.
22. X.S. Yang, Metaheuristic optimization: algorithm analysis and open problems, in: P. Pardalos, S. Rebennack (Eds.), Experimental Algorithms, Lecture notes in Computer Science, vol. 6630, Springer Verlag, Berlin, 2011, pp. 21–32.
23. X.S. Yang, Firefly algorithm, levy flights and global optimization, in: M. Bramer, R. Ellis, M. Petridis (Eds.), Research and Development in Intelligent Systems XXVI, Springer, 2010, pp. 209–218.
24. X.S. Yang, Efficiency analysis of swarm intelligence and randomization techniques, Journal of Computational and Theoretical Nanoscience 9 (2) (2012) 189–198.
25. J. Holland, Adaptation in Natural and Artificial Systems, 1st edition, MIT Press, Cambridge, USA, 1992.
26. J. Kennedy, R. Eberhart, The particle swarm optimization: social adaptation in information processing, in: D. Corne, M. Dorigo, F. Glover (Eds.), New Ideas  in Optimization, McGraw Hill, London, UK, 1999, pp. 379–387.
27. I. Fister et al. in Swarm and Evolutionary Computation 13 (2013), pp. 34–46
28. R. Mallipeddi, P. Suganthan, Q. Pan, M. Tasgetiren, Differential evolution  algorithm with ensemble of parameters and mutation strategies, Applied Soft Computing 11 (2) (2011) 1679–1696.