Bi-Section Algorithm for Solving Linear Bi-Level Programming Problem
Eghbal Hosseini1, *, Isa Nakhai Kamalabadi2
1Department of Mathematics, Payamenur University of Tehran, Tehran, Iran
2Department of Industry, University of Kurdistan, Sanandaj, Iran
Abstract
The bi-level programming problem (BLPP) is significant because of its application in several areas such as transportation, finance, management, computer science and so on. This problem is an appropriate tool to model these real problems. It has been proven that the general BLPP is an NP-hard problem. Therefore, the BLPP is a practical and complicated problem so solving this problem would be significant. In this paper, we attempt for developing an algorithm based on bi-section algorithm to solve BLPP. Using the Karush-Kuhn-Tucker conditions the bi-level programming problem is converted to a non-smooth single level problem, and then it is smoothed by heuristic method for using proposed bi-section algorithm. The smoothed problem is solved using bi-section algorithm which is an exact method for solving the problem. The presented approach achieves an efficient and feasible solution in an appropriate time which has been evaluated by solving test problems.
Keywords
Bi-Section Algorithm, Linear Bi-Level Programming Problem, Karush-Kuhn-Tucker Conditions
Received:April 17, 2015
Accepted: May 8, 2015
Published online: June 14, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
It has been proven that the bi-level programming problem (BLPP) is an NP-Hard problem [1,2]. Several algorithms have been proposed to solve BLPP [11,12,13,21,25,26,27,28,29,31,32,33]. These algorithms are divided into the following classes: global techniques, enumeration methods, transformation methods [3,4,22,23], meta heuristic approaches, fuzzy methods [5,6,7,8,24], primal-dual interior methods [13]. In the following, these techniques are shortly introduced.
1.1. Global Techniques
All optimization methods can be divided into two distinctive classes: local and global algorithms. Local ones depend on initial point and characteristics such as continuity and differentiability of the objective function. These algorithms search only a local solution, a point at which the objective function is smaller than at all other feasible points in vicinity. They do not always find the best minima, that is, the global solution. On the other hand, global methods can achieve global optimal solution. These methods are independent of initial point as well as continuity and differentiability of the objective function [9,10,11,12,34,35].
1.2. Enumeration Methods
Branch and bound is an optimization algorithm that uses the basic enumeration. But in these methods we employ clever techniques for calculating upper bounds and lower bounds on the objective function by reducing the number of search steps. In these methods, the main idea is that the vertex points of achievable domain for BLPP are basic feasible solutions of the problem and the optimal solution is among them [14].
1.3. Meta Heuristic Approaches
Meta heuristic approaches are proposed by many researchers to solve complex combinatorial optimization. Whereas these methods are too fast and known as suitable techniques for solving optimization problems, however, they can only propose a solution near to optimal. These approaches are generally appropriate to search global optimal solutions in very large space whenever convex or non-convex feasible domain is allowed. In these approaches, BLPP is transformed to a single level problem by using transformation methods and then meta- heuristic methods are utilized to find out the optimal solution [15,16,17,18,19,25,36,40].
However there are several approaches to solve optimization problems, but there is no any exact classic approach. In this paper, the authors have tried to proposed bi-section algorithm, which is a convergent approach, to solve linear BLPP.
The remainder of the paper is structured as follows: problem formulation and smoothing method to the BLPP are introduced in Section 2. The algorithm based on bi-section is proposed in Section 3. Computational results are presented for our approaches in Section 4. As result, the paper is finished in Section 5 by presenting the concluding remarks.
2. Problem Formulation and Smoothing Method
It has been proven that the bi-level programming problem (BLPP) is an NP-Hard problem [1,2]. Several algorithms have been proposed to solve BLPP [11,12,13,21,25,26,27,28,29,31,32,33]. These algorithms are divided into the following classes: global techniques [9,10,11,12,34,35], enumeration methods [14], transformation methods, meta heuristic approaches, fuzzy methods [5,6,7,8,24], primal-dual interior methods [13]. In the following, these techniques are shortly introduced.
The BLPP is used frequently by problems with decentralized planning structure. It is defined as [20]:
|
| (1) |
Definition 2.1:
Every point such as ![]() is an optimal solution to the bi-level problem if
is an optimal solution to the bi-level problem if
![]() (2)
(2)
Which IR is feasible region of the BLPP.
Using KKT conditions problem (1) can be converted into the following problem:
|
| (3) |
To convert the inequality constraint to an equality constraint, the positive slack variable ![]() is added:
is added:
|
| (4) |
3. Bi-section Algorithm (BA)
Most of nonlinear equations are very difficult to solve and some of them are unsolved. Therefore several methods have been proposed to approximate of the root these nonlinear equations. One of the most important methods to approximate the root is the bi-section algorithm. Necessary condition to use these methods, to find approximate of root, is the uniqueness root of the nonlinear equation [41, 42]. Firstly we proposed necessary definitions and theorems then explain the bi-section algorithm. Finally to illustrate this method we solve several examples.
Definition 3.1:
![]() , that
, that ![]() is limit points of A.
is limit points of A.
Definition 2:
![]() are separated if
are separated if ![]()
Definition 2.2:
A is a connected set if it is not union of two separated sets.
The following theorems guarantee that the equation ![]() has just a root.
has just a root.
Theorem1 [43]
If f be a continuous function in closed interval [a,b] and f(a)f(b)<0 then f(x)=0 has at least a root in (a,b).
Proof:
Because f is continuous then f([a,b]) is connected [3]. Let ![]() if there is no any x so that f(x)=0 then
if there is no any x so that f(x)=0 then ![]() .
.
Now let ![]()
![]()
![]()
Also A , B are separated then E is not connected and this is opposite assumption. Then proof is complete.
Now we proposed a theorem without proof.
Theorem 2 [43]
If f be a continuous function in closed interval [a,b] and differentiable function in (a,b) then f(x)=0 has at most a root in (a,b).
Example 1:
Let ![]()
We check two theorems to this function.
f is continuous function and ![]() because:
because:
![]()
![]()
Then ![]() has at least one root in given interval according theorem 1.
has at least one root in given interval according theorem 1.
![]() Obviously
Obviously![]() therefore f has at most one root in given interval.
therefore f has at most one root in given interval.
The bisection method is a simple method to find a root of equation in an interval. Suppose f is a continuous function in interval [a,b] and f(a)f(b)<0, we want approximate root of f(x) = 0. The root of f(x) =0 in interval [a,b] should be unique namely two theorem 1 and 2 should applicable to the f(x)=0 in interval [a,b]. In this method, first of all the interval [a,b] is bisected, let ![]() , at the next step we check signs of f(a)f(c) and f(c)f(b), if f(a)f(c)<0 then the subinterval [a,c] is selected and we sets b=c and if f(c)f(b)<0 the subinterval [c,b] is selected and we sets a=c. Definitely in both of two cases, the sign of f(a)f(b) is negative therefore the bisection algorithm is applicable to new interval [a,b]. This procedure is continued while one of the under conditions is true.
, at the next step we check signs of f(a)f(c) and f(c)f(b), if f(a)f(c)<0 then the subinterval [a,c] is selected and we sets b=c and if f(c)f(b)<0 the subinterval [c,b] is selected and we sets a=c. Definitely in both of two cases, the sign of f(a)f(b) is negative therefore the bisection algorithm is applicable to new interval [a,b]. This procedure is continued while one of the under conditions is true.
1. ![]() , which
, which ![]() are the midpoint of the interval in (n+1)th step and root respectively.
are the midpoint of the interval in (n+1)th step and root respectively.
2. ![]() , which
, which ![]() are the midpoint of the interval in (n+1)th and nth step.
are the midpoint of the interval in (n+1)th and nth step.
3. ![]() , which
, which![]() is a given very small and positive number in all conditions.
is a given very small and positive number in all conditions.
However bisection algorithm is a simple method, but it obtain solution very slowly. Therefore an approximation of solution is obtained by this method then it is used in other methods as a starting point.
In the bi-section method a sequence is composed so that limit of the sequence is equal to root of the given equation.
Steps
Step1: input a,b.
Step 2: let x = (a+b)/2 : print x.
Step 3: if ABS (f(x)) <EPS then end.
Step 4: if f (a) f(x)<0 then let b=x ELSE let a=x.
Step 5: GOTO 2.
Step 6: END.
Theorem 3
The bi-section method is convergent in the interval [a,b] if f(a)f(b)<0 and f is continuous.
Proof: if ![]() is the midpoint of the interval in the ith step and p is solution, then absolute error in iterations is:
is the midpoint of the interval in the ith step and p is solution, then absolute error in iterations is:
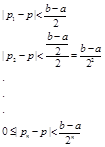
As we now![]() Consequently we have:
Consequently we have:
![]() .
.
Therefore the composed sequence by the bi-section algorithm is convergent to the root f.
Example 2
Suppose we are going to solve the simple equation by the bi-section algorithm.
![]()
To solve this equation firstly we manipulate it that right side be zero. Then we have
![]()
Equivalently the goal is finding root of function
![]()
Now we guess two number such as a,b so that ![]() . Let a=0 and b=1 then f(a)=-1 and f(b)=1 therefore
. Let a=0 and b=1 then f(a)=-1 and f(b)=1 therefore![]() .
.
Because f is polynomial then it is continuous in every interval of real numbers particularly in [0, 1]. Therefore f has conditions of theorem 1 then f has at least one root in [0, 1].
Derivative of f equal to:
![]()
Obviously ![]() is positive in (0, 1) therefore
is positive in (0, 1) therefore ![]() then f has conditions of theorem 2 too. Namely f(x) =0 has at most a root in (0, 1).
then f has conditions of theorem 2 too. Namely f(x) =0 has at most a root in (0, 1).
According to the theorem 1 and theorem 2, f(x) =0 has just one root in (0, 1). Now we con use the bi-section algorithm to find the root of ![]() in interval [0, 1].
in interval [0, 1].
The following table is summary of the bi-section method to solve this example at the five iterations:
Table 1. Stages of bi-section algorithm-Example 2.
| Iterations | a | b | sign of | |
| 1 | 0 | 1 | 0.5 |
|
| 2 | 0.5 | 1 | 0.75 | _ |
| 3 | 0.5 | 0.75 | 0.6258 | - |
| 4 | 0.5 | 0.625 | 0.5625 | + |
| 5 | 0.625 | 0.625 | 0.5937 |
According the above table root of ![]() in [0, 1] approximately is
in [0, 1] approximately is ![]() .
.
Example 3
Suppose we are going to approximate the root of following equation by the bi-section algorithm until![]()
![]()
In fact we want finding root of function ![]() .
.
Now we guess two number such as a,b so that ![]() . Let a=0 and b=1 then f(a)=-1 and f(b)=1 therefore
. Let a=0 and b=1 then f(a)=-1 and f(b)=1 therefore
![]() .
.
Because f is polynomial then it is continuous in every interval of real numbers particularly in [0, 1]. Therefore f has conditions of theorem 1 then f has at least one root in [0, 1].
Derivative of f equal to:
![]()
Obviously ![]() is positive in (0, 1) therefore f has conditions of theorem 2 too. Namely f(x) =0 has at most a root in (0, 1).
is positive in (0, 1) therefore f has conditions of theorem 2 too. Namely f(x) =0 has at most a root in (0, 1).
According to the theorem 1 and theorem 2, f(x) =0 has just one root in (0, 1). Now we con use the bi-section algorithm to find the root of ![]() in interval [0, 1].
in interval [0, 1].
The following table is summary of the bi-section method to solve this example at the five iterations:
Table 2. Stages of bi-section algorithm-Example 3.
| Iterations | a | b | sign of | ||
| 1 | 0 | 1 | 0.5 | _ | 0.2167 |
| 2 | 0 | 0.5 | 0.25 | + | 0.1748 |
| 3 | 0.25 | 0.5 | 0.375 | _ | 0.0452 |
| 4 | 0.25 | 0.375 | 0.3125 | + | 0.0559 |
| 5 | 0.3125 | 0.375 | 0.3437 | + | 0.0035 |
According the above table root of ![]() in [0, 1] approximately is
in [0, 1] approximately is ![]() .
.
4. Computational Results
To illustrate bi-section algorithm, two standard examples will be solved in this section.
Example 4 [17]
Consider the following linear bi-level programming problem:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Using KKT conditions, the following problem is obtained:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This problem have been solved using bi-section algorithm, Optimal solution have been presented according to Table 3.
Table 3. Comparison of optimal solutions by hybrid algorithm-Example 4.
| Best solution by our method | Best solution according to reference [17] | Optimal solution | |||
| ( |
|
|
|
|
|
| (4,4) | -12 | (3.9,4) | -12.1 | (4,4) | -12 |
Example 5 [17]
Consider the following linear bi-level programming problem.
![]()
![]()
![]()
![]()
![]()
![]()
After applying KKT conditions and smoothing method, the above problem will be transformed into the problem which will be solved using bi-section algorithm. Optimal solution for this example is presented according to Table 4.
More problems with deferent sizes have been solved by two approaches and computation results have been proposed in Table 5. The programming is performed using MATLAB 7.1 and use a personal computer (CPU: Intel (R) Celeron(R) 1000 M @ 1.8 GHz, RAM: 4 GB) to execute the program. It is easy to see that TA algorithm is better than HA according to Table 6.
Table 4. Comparison of optimal solutions by hybrid algorithm-Example 5.
| Best solution by our method | Best solution according to reference [17] | Optimal solution | |||
| ( |
|
|
|
|
|
| (1.88.,0.79,0.09) | 8.40 | (1.83,0.89,0.004) | 8.21 | ( | 8.44 |
Table 5. Comparison of optimal solutions and elapsed time with different examples 6-9 of BLPP by Taylor algorithm
| Best solution by our method with different values of ε | Best solution according to reference [3,7,26,27] | |
| O.S | O.S | |
| Example 6 | (1.33,1.30,0.03,0.37,1.30,0.91) | (1.32,1.28,0,0.33,1.25,0.92) |
| Example 7 | (2,0,0,0) | (2,0,0,0) |
| Example 8 | (0,1,0.2,0.6,0.4) | (0,0.9,0,0.6,0.4) |
| Example 9 | (17,11.04) | (17.45,10.90) |
5. Conclusion and Future Work
The main difficulty of the multi-level programming problem is that after using the KKT conditions the non-linear constraints are appeared. In this paper was attempted to remove these constraints by the proposed theorem, slack variables and proposed PSOMGA algorithm. As mentioned previously the authors have been combined two continuous and discrete effective approaches to the linear BLPP which this form of combining has not been studied by any researchers. According to the Tables the proposed method presents optimal solution in appropriate time and iterations. In the future works, the following should be researched:
(1) Examples in the larger sizes can be supplied to illustrate the efficiency of the proposed algorithm.
(2) Showing the efficiency of the proposed algorithm for solving other kinds of BLPP such as quadratic and non-linear.
(3) Solving other kinds of multi-level programming problem such as tri-level programming problem.
Nomenclature
|
| Objective function of the first level in the TLPP |
|
| Objective function of the second level in the TLPP |
|
| Objective function of the third level in the TLPP |
|
| Constraints in the TLPP |
|
| Slack variable |
|
| Slack variable |
|
| Objective function of the first level in the BLPP |
|
| Objective function of the first level in the BLPP |
|
| Constraints in the BLPP |
|
| A nonempty convex set |
|
| Lagrange function |
|
| Lagrange Coefficient |
|
| Lagrange Coefficient |
|
| Lagrange Coefficient |
|
| Initial population |
|
| Crossover population |
|
| Mutation population |
|
| Set of chromosomes in the current generation |
|
| Optimal solution for the TLPP |
|
| Optimal solution for the BLPP |
References
- J.F. Bard, Some properties of the bi-level linear programming, Journal of OptimizationTheory and Applications (1991) 68 371–378.
- L. Vicente, G. Savard, J. Judice, Descent approaches for quadratic bi-level programming, Journal of Optimization Theory and Applications (1994) 81 379–399.
- Lv. Yibing, Hu. Tiesong, Wang. Guangmin, A penalty function method Based on Kuhn–Tucker condition for solving linear bilevel programming, Applied Mathematics and Computation (2007) 1 88808–813.
- G. B. Allende, G. Still, Solving bi-level programs with the KKT-approach, Springer and Mathematical Programming Society (2012) 1 31:37 – 48.
- M. Sakava, I. Nishizaki, Y. Uemura, Interactive fuzzy programming for multilevel linear programming problem, Computers & Mathematics with Applications (1997) 36 71–86.
- S Sinha, Fuzzy programming approach to multi-level programming problems, Fuzzy Sets and Systems (2003) 136 189–202.
- S. Pramanik, T.K. Ro, Fuzzy goal programming approach to multilevel programming problems, European Journal of Operational Research (2009) 194 368–376.
- S.R. Arora, R. Gupta, Interactive fuzzy goal programming approach for bi-level programming problem, European Journal of Operational Research (2007) 176 1151–1166.
- J. Nocedal, S.J. Wright, 2005 Numerical Optimization, Springer-Verlag, New York.
- A.AL Khayyal, Minimizing a Quasi-concave Function Over a Convex Set: A Case Solvable by Lagrangian Duality, proceedings, I.E.E.E. International Conference on Systems, Man,and Cybemeties, Tucson AZ (1985) 661-663.
- R. Mathieu, L. Pittard, G. Anandalingam, Genetic algorithm based approach to bi-level Linear Programming, Operations Research (1994) 281–21.
- G. Wang, B. Jiang, K. Zhu, (2010) Global convergent algorithm for the bi-level linear fractional-linear programming based on modified convex simplex method, Journal of Systems Engineering and Electronics 239–243.
- W. T. Wend, U. P. Wen, (2000) A primal-dual interior point algorithm for solving bi-level programming problems, Asia-Pacific J. of Operational Research, 17.
- N. V. Thoai, Y. Yamamoto, A. Yoshise, (2002) Global optimization method for solving mathematical programs with linear complementary constraints, Institute of Policy and Planning Sciences, University of Tsukuba, Japan 978.
- S.R. Hejazi, A. Memariani, G. Jahanshahloo, (2002) Linear bi-level programming solution by genetic algorithm, Computers & Operations Research 29 1913–1925.
- G. Z. Wang, Wan, X. Wang, Y.Lv, Genetic algorithm based on simplex method for solving Linear-quadratic bi-level programming problem, Computers and Mathematics with Applications(2008) 56 2550–2555.
- T. X. Hu, Guo, X. Fu, Y. Lv, (2010) A neural network approach for solving linear bi-level programming problem, Knowledge-Based Systems 23 239–242.
- B. Baran Pal, D .Chakraborti, P. Biswas, (2010) A Genetic Algorithm Approach to Fuzzy Quadratic Bi-level Programming, Second International Conference on Computing, Communication and Networking Technologies.
- Z. G.Wan, Wang, B. Sun, (2012) A hybrid intelligent algorithm by combining particle Swarm optimization with chaos searching technique for solving nonlinear bi-level programming Problems, Swarm and Evolutionary Computation.
- J.F. Bard, Practical bi-level optimization: Algorithms and applications, Kluwer Academic Publishers, Dordrecht, 1998.
- J.F. Bard, Some properties of the bi-level linear programming, Journal of Optimization Theory and Applications 68 (1991) 371–378.
- S Hosseini, E & I.Nakhai Kamalabadi.Line Search and Genetic Approaches for Solving Linear Tri-level Programming Problem International Journal of Management, Accounting and Economics Vol. 1, No. 4, 2014.
- S Hosseini, E & I.Nakhai Kamalabadi. aylor Approach for Solving Non-Linear Bi-level Programming Problem ACSIJ Advances in Computer Science: an International Journal, Vol. 3, Issue 5, No.11 , September. 5.
- S Hosseini, E & I.Nakhai Kamalabadi.Two Approaches for Solving Non-linear Bi-level Programming Problem, Advances in Research Vol. 4, No.3, 2015. ISSN: 2348-0394
- J. Yan, Xuyong.L, Chongchao.H, Xianing.W, Application of particle swarm optimization based on CHKS smoothing function for solving nonlinear bi-level programming problem, Applied Mathematics and Computation 219 (2013) 4332–4339.
- Xu, P, & L. Wang. An exact algorithm for the bilevel mixed integer linear programming problem under three simplifying assumptions, Computers & Operations Research, Volume 41, January, Pages 309-318 (2014).
- Wan, Z, L. Mao, & G. Wang. Estimation of distribution algorithm for a class of nonlinear bilevel programming problems, Information Sciences, Volume 256, 20 January, Pages 184-196(2014).
- Zheng, Y, J. Liu, & Z. Wan. Interactive fuzzy decision making method for solving bi-level programming problem, Applied Mathematical Modelling, Volume 38, Issue 13, 1 July, Pages 3136-3141(2014).
- Zhang, G, J. Lu, J. Montero, & Y. Zeng, Model. solution concept, and Kth-best algorithm for linear tri-level, programming Information Sciences 180 481–492 (2010) .
- A. Silverman. Richard, Calculus with analytic geometry, ISBN:978-964-311-008-6, 2000.
- Y. Zheng, J. Liu, Z. Wan, Interactive fuzzy decision making method for solving bi-level programming problem, Applied Mathematical Modelling, Volume 38, Issue 13, 1 July 2014, Pages 3136-3141.
- Y. Jiang, X. Li, C. Huang, X. Wu, An augmented Lagrangian multiplier method based on a CHKS smoothing function for solving nonlinear bi-level programming problems, Knowledge-Based Systems, Volume 55, January 2014, Pages 9-14.
- X. He, C. Li, T. Huang, C. Li, Neural network for solving convex quadratic bilevel programming problems, Neural Networks, Volume 51, March 2014, Pages 17-25.
- Z. Wan, L. Mao, G. Wang, Estimation of distribution algorithm for a class of nonlinear bilevel programming problems, Information Sciences, Volume 256, 20 January 2014, Pages 184-196.
- P. Xu, L. Wang, An exact algorithm for the bilevel mixed integer linear programming problem under three simplifying assumptions, Computers & Operations Research, Volume 41, January 2014, Pages 309-318.
- E. Hosseini, I.Nakhai Kamalabadi, A Genetic Approach for Solving Bi-Level Programming Problems, Advanced Modeling and Optimization, Volume 15, Number 3, 2013.
- E. Hosseini, I.Nakhai Kamalabadi, Solving Linear-Quadratic Bi-Level Programming and Linear-Fractional Bi-Level Programming Problems Using Genetic Based Algorithm, Applied Mathematics and Computational Intelligence, Volume 2, 2013.
- E. Hosseini, I.Nakhai Kamalabadi, Taylor Approach for Solving Non-Linear Bi-level ProgrammingProblem ACSIJ Advances in Computer Science: an International Journal, Vol. 3, Issue 5, No.11, September 2014.
- E. Hosseini, I.Nakhai Kamalabadi, Solving Linear Bi-level Programming Problem Using Two New Approaches Based on Line Search International Journal of Management sciences and Education, Vol. 2, Issue 6, 2014, 243-252.
- E. Hosseini, I.Nakhai Kamalabadi, Two Approaches for Solving Non-linear Bi-levelProgramming Problem, Advances in Research, 3(5), 2015.
- Froberg,carl-Erik. Numerical Mathematics, Theory and Computer Applications. The Benjamin Publishing Company, 1985.
- Hamming, R.W. numerical methods for scientists and engineers. Mc Graw-Hill, New York, 1962.
- Walter Rudin, Principles of Mathematical Analysis, 3rd ed. McGraw-Hill, New York, 1976.



